Annuity

How to Calculate the Present Value of an Annuity

An annuity provides periodic payments for a specific number of years until reaching maturity.

Annuities are a distinct type of financial security because of the following characteristics:

• Periodic Payments → Annuities are a common source of retirement income because the securities offer the issuer a steady stream of payments issued at regular intervals.
• No Lump Sum Principal Repayment → Unique to annuities, there is no final lump sum payment (i.e. the principal) paid back at the end of the borrowing term, similar to zero-coupon bonds.
• Predefined Maturity Date → Unlike a perpetuity, an annuity also comes with a pre-determined maturity date, which marks the date when the final interest payment is received.
• Equal Installment Payments → Since there is no final principal repayment, each payment is equal in value. However, payments received earlier are more valuable due to the “time value of money.”

Earlier cash flows can be reinvested earlier and for a longer duration, so these cash flows carry the highest value (and vice versa for cash flows received later).

Typically, the most common types of issuers of annuities are the following:

• Insurance Companies (e.g. Retirement Planning)
• Mutual Funds
• Brokerage Firms
• Mortgage and Auto Financing

Present Value of Annuity Formula (PV)

The present value (PV) of an annuity is the discounted value of the bond’s future payments, adjusted by an appropriate discount rate, which is necessary because of the time value of money (TVM) concept.

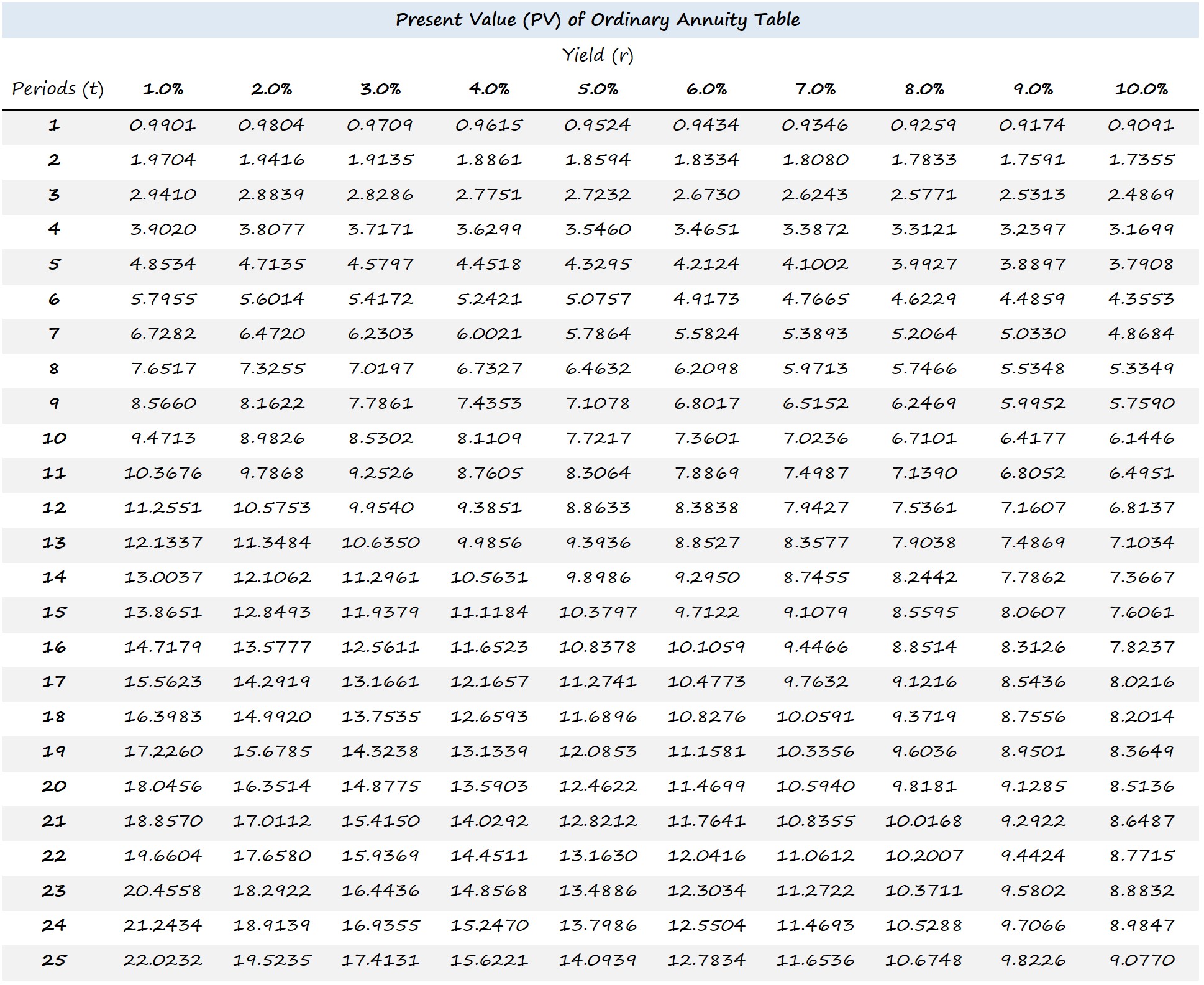
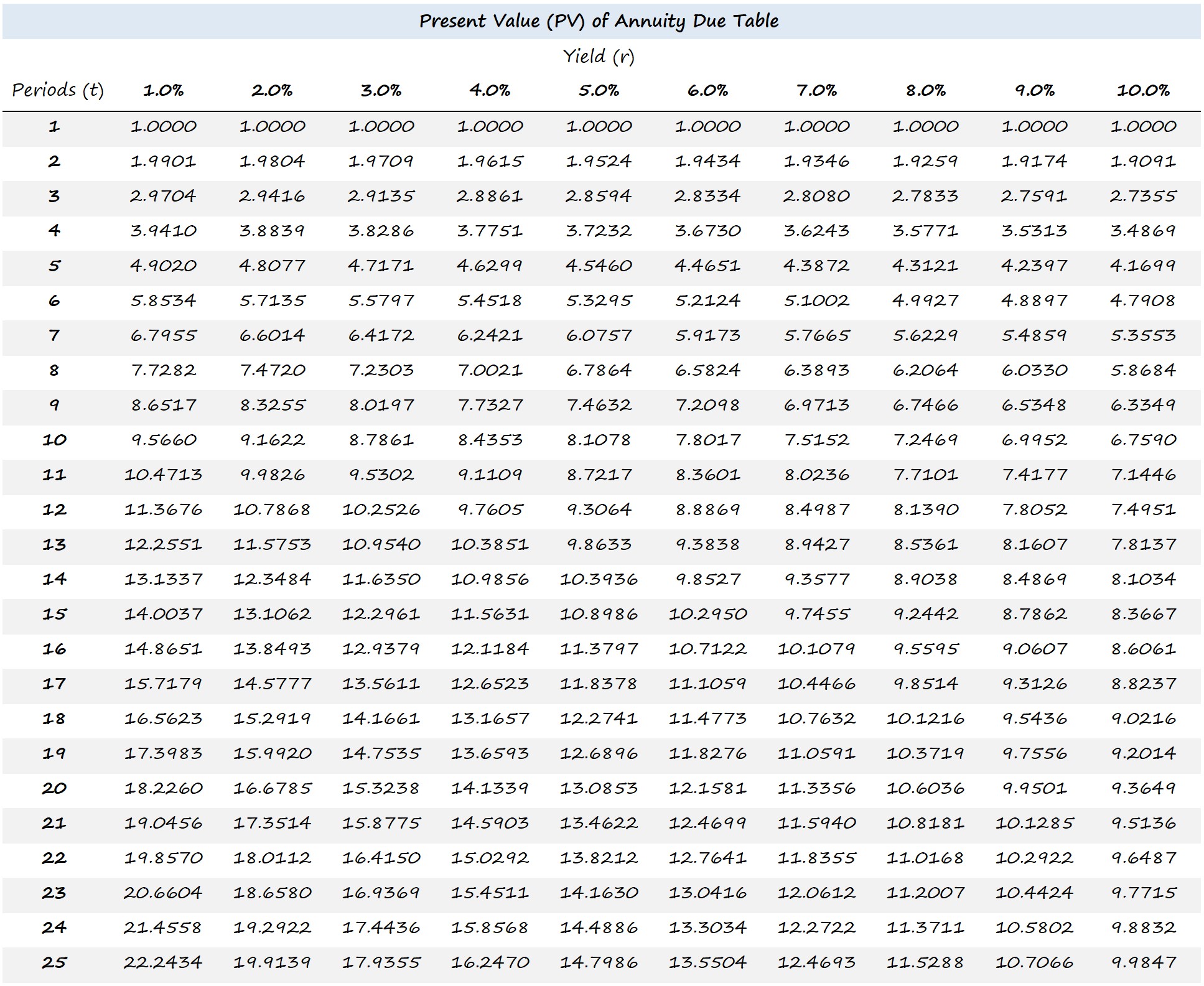
The formula to calculate the present value (PV) of an annuity is equal to the sum of all future annuity payments – which are divided by one plus the yield to maturity (YTM) and raised to the power of the number of periods.

Where:

• PV = Present Value
• A = Annuity Payment Per Period ($)
• t = Number of Periods
• r = Yield to Maturity (YTM)

Alternatively, a simpler approach consists of the following two steps:

1. First, the annuity payment is divided by the yield to maturity (YTM), denoted as “r” in the formula.
2. Next, the result from the previous step is multiplied by one minus [one divided by (one + r) raised to the power of the number of periods].

Ordinary Annuity vs. Annuity Due: What is the Difference?

When calculating the present value (PV) of an annuity, one factor to consider is the timing of the payment.

• Ordinary Annuity → Cash Flows Received at End of Period
• Annuity Due → Cash Flows Received at Beginning of Period

The term “annuity due” means receiving the payment at the beginning of each period (e.g. monthly rent).

On the other hand, an “ordinary annuity” is more so for long-term retirement planning, as a fixed (or variable) payment is received at the end of each month (e.g. an annuity contract with an insurance company).

• Fixed Annuity → The insurance company provides interest in the form of periodic payments that must meet the minimum rate of return threshold.
• Variable Annuity → The insurance company allows owners to allocate their annuity payments into certain low-risk investment vehicles, such as mutual funds.

The trade-off with fixed annuities is that an owner could miss out on any changes in market conditions that could have been favorable in terms of returns, but fixed annuities do offer more predictability.

Present Value of an Ordinary Annuity Table (PV)

Present Value of an Annuity Due Table (PV)

Present Value (PV) of Annuity Calculator

We’ll now move to a modeling exercise, which you can access by filling out the form below.

Get the Excel Template!

First Name *

Email *

Submit

By submitting this form, you consent to receive email from Wall Street Prep and agree to our terms of use and privacy policy.

Email provided

Your Download is Ready

Submitting...

1. Annuity Bond Assumptions

In our illustrative example, we’ll calculate an annuity’s present value (PV) under two different scenarios.

1. Ordinary Annuity
2. Annuity Due

The assumptions listed below are to be used for the entirety of the exercise.

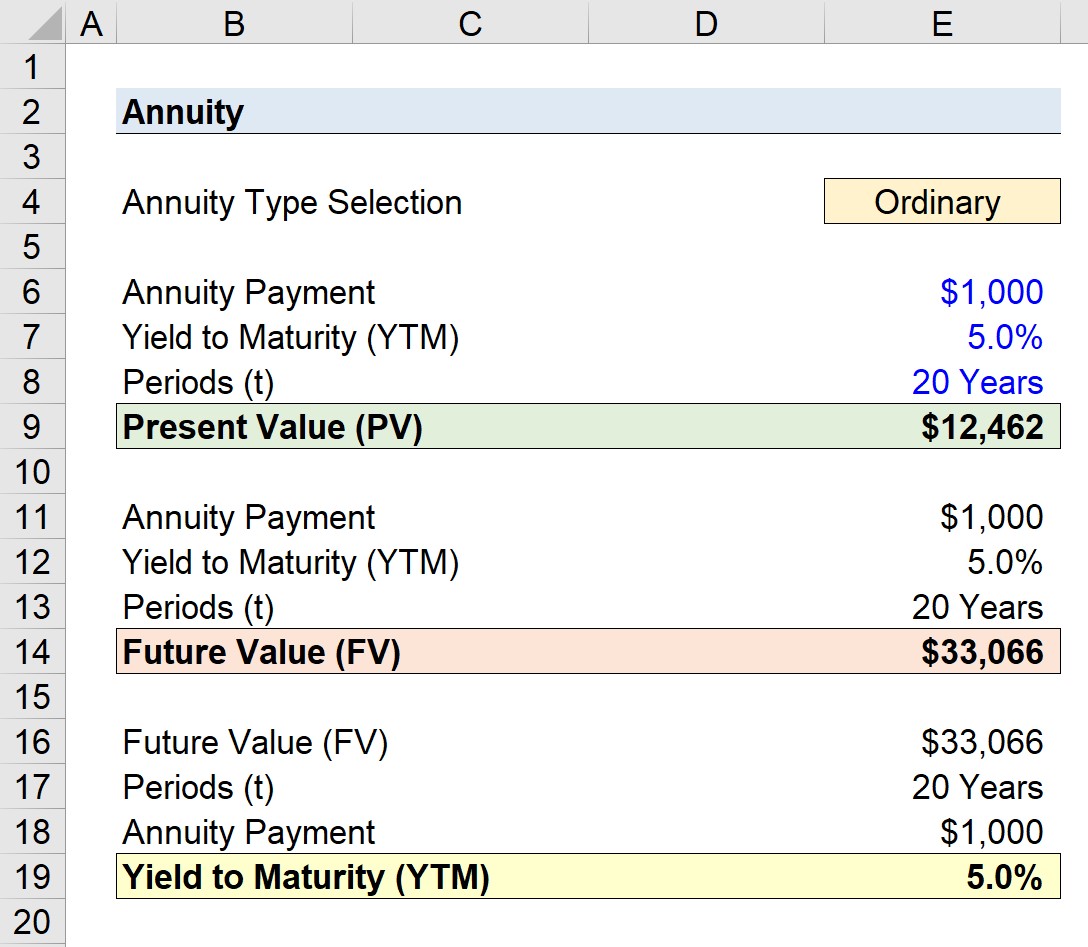
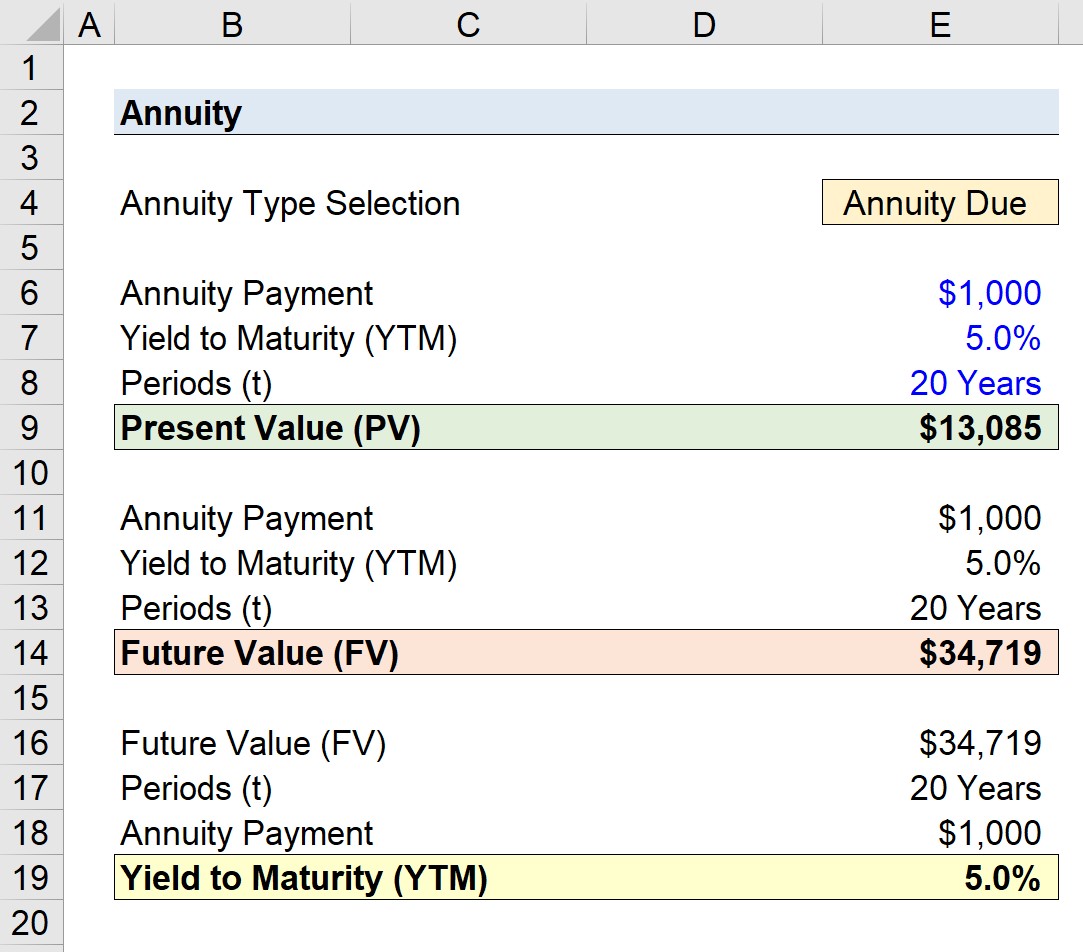
• Annuity Payment = $1,000
• Yield (r) = 5.0%
• Periods (t) = 20 Years

2. Present Value of Annuity Calculation Example (PV)

First, we will calculate the present value (PV) of the annuity given the assumptions regarding the bond.

The “PV” Excel function can be used here, as shown below.

• Present Value (PV) = PV (r, Periods, – Annuity Payment, 0, “0” or “1”)
• Present Value (PV) = PV (5%, 20, –$1,000, 0, IF (Annuity Type Cell =“Ordinary”,0,1))

Note: Since we have two scenarios, we’ll create a toggle to alternate between the two options – which is the “IF(Annuity Type Cell =“Ordinary,” 0,1)”.

The two present value (PV) amounts calculated on the annuity bond are the following:

• Ordinary Annuity = $12,462
• Annuity Due = $13,085

3. Future Value of Annuity Calculation Example (FV)

From there, we can also calculate the future value (FV) using the formula below:

• Future Value (FV) = – FV (r, t, Annuity Payment, 0, “0” or “1”)
• Future Value (FV) = – FV (5%, 20, $1,000, 0, IF (E5 = “Ordinary”, 0, 1))

The two future value (FV) amounts calculated on the annuity bond are the following:

• Ordinary Annuity = $33,066
• Annuity Due = $34,719

We’ll calculate the yield to maturity (YTM) using the “RATE” Excel function in the final step.

• Yield to Maturity (YTM) = RATE (t, Annuity Payment, 0, – FV, “0” or “1”)
• Yield to Maturity (YTM) = RATE (20, $1,000, 0, – FV, IF (E5 = “Ordinary”, 0, 1))”

In conclusion, the annuity bond has a yield of 5.0% under either scenario.

^{Ordinary Annuity}

^{Annuity Due}