What is Marginal Revenue?
Marginal Revenue represents the incremental change – either positive or negative – in a company’s revenue from selling one more unit.
The production and sale of an additional unit tend to continue to generate more revenue, but only until a certain level of production volume is reached, above which the benefits start to reverse course.

How to Calculate Marginal Revenue
The marginal revenue measures the increase (or decrease) in revenue from the sale of an additional unit of product.
Conceptually, marginal revenue represents the additional revenue from the sale of another unit of output, i.e. the extra revenue brought in from each sale.
From the perspective of management, marginal analysis enables them to determine their company’s optimal output level and adjust accordingly, as profit maximization and the management of costs are critical components of a properly functioning, sustainable business model.
In accordance with the law of diminishing returns, the marginal benefit per unit should theoretically start to decline at a certain point, where the marginal cost per unit offsets the benefits from higher levels of output.
Therefore, companies carry an economic incentivize to optimize their production volume until the marginal benefits are close to being fully maximized, yet any more volume beyond that is risky because the benefits will then start to wane.
If all other factors are kept constant, each additional unit of input before reaching the inflection point causes the marginal benefit to rise.
Beyond the point at which the revenue received by the sale of each extra unit of output is positive, the marginal benefit soon becomes detrimental, resulting in fewer profits (and lower profit margins).
The intersection at which this occurs is the point where the marginal benefit equals the marginal cost.
- Marginal Benefit → The change in the total monetary benefits arising from the increased output.
- Marginal Cost → The change in the total costs arising from the increased output.
Past this point, the marginal costs outweigh the marginal benefit (and the demand curve becomes downward sloping for that specific reason).
The Wharton Online & Wall Street Prep Applied Value Investing Certificate Program
Learn how institutional investors identify high-potential undervalued stocks. Enrollment is open for the Oct 6 - Nov 30 cohort.
Enroll TodayMarginal Revenue Formula
The formula for calculating the marginal revenue is as follows.
Where:
- Change in Revenue = Ending Revenue – Beginning Revenue
- Change in Quantity = Ending Quantity – Beginning Quantity
The change in revenue and the change in quantity are the two inputs necessary to compute the marginal benefit, and both of the variables equal the end-of-period balance minus the beginning-of-period balance.
- Change in Revenue (Δ) → The increase or decrease in a company’s revenue in dollar terms across a specified period.
- Change in Quantity (Δ) → The increase or decrease in the number of production units for sale in the corresponding period.
Marginal Revenue Calculator
We’ll now move to a modeling exercise, which you can access by filling out the form below.
Marginal Revenue Calculation Example
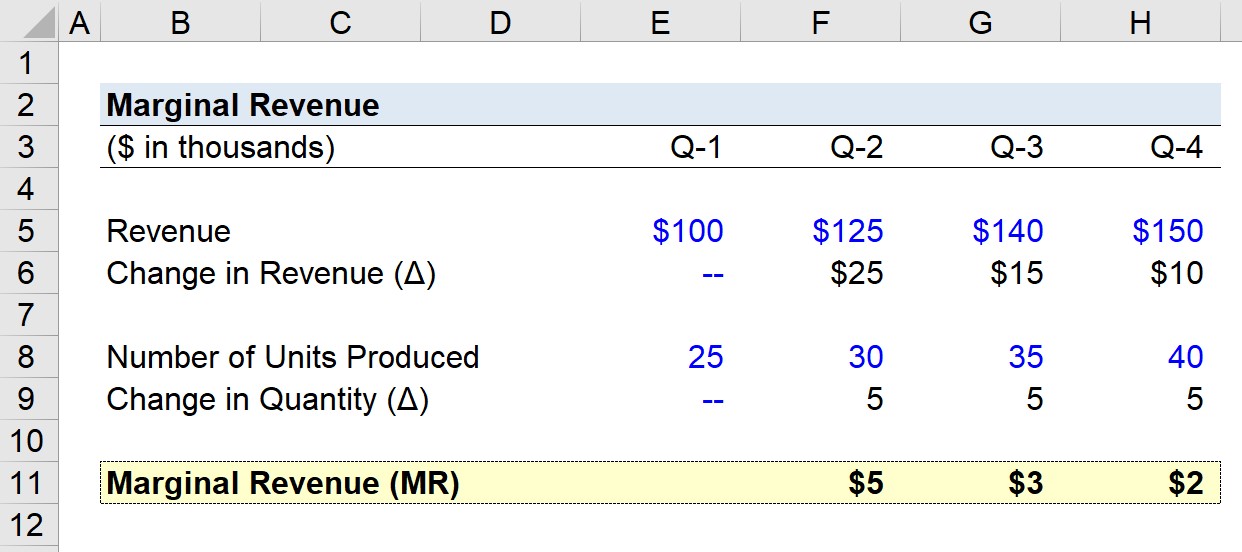
Suppose a company generated the following quarterly revenue figures over the past year.
- Q-1 Revenue = $100k
- Q-2 Revenue = $125k
- Q-3 Revenue = $140k
- Q-4 Revenue = $150k
In ascending order from Q-1 to Q-4, the quarterly change in revenue is as follows:
- Quarterly Revenue Growth, Q-1 to Q-2 = $25k
- Quarterly Revenue Growth, Q-2 to Q-3 = $15k
- Quarterly Revenue Growth, Q-3 to Q-4 = $10k
The pace of growth in our company’s revenue is declining each quarter based on the trend seen above.
Our assumptions regarding the number of units produced per quarter are as follows.
- Q-1 Number of Units Produced = 25k
- Q-2 Number of Units Produced = 30k
- Q-3 Number of Units Produced = 35k
- Q-4 Number of Units Produced = 40k
The quarterly change in quantity remains fixed at 5k, as evident in the pattern.
Since we have the required inputs to calculate the marginal revenue of our hypothetical company, our final step is to divide the change in revenue by the change in quantity for each quarter, except for Q-1.
- Marginal Revenue, Q-1 to Q-2 = $5k
- Marginal Revenue, Q-2 to Q-3 = $3k
- Marginal Revenue, Q-3 to Q-4 = $2k
The gradual reduction in the marginal revenue from $5k to $2k by the end of Q-4 reflects the law of diminishing returns, wherein the marginal benefits decline as more units are produced.
Marginal Revenue vs. Marginal Cost: What is the Difference?
While the concept of marginal revenue (MR) is the incremental monetary benefits obtained by increasing the quantity by one unit, the marginal cost (MC) is the incremental loss incurred from increasing the quantity by a unit.
If the marginal revenue exceeds the marginal cost, then there are still residual profits attainable from greater production volume.
Taken together, marginal revenues and marginal costs are both tracked in order for companies to maximize their profits.
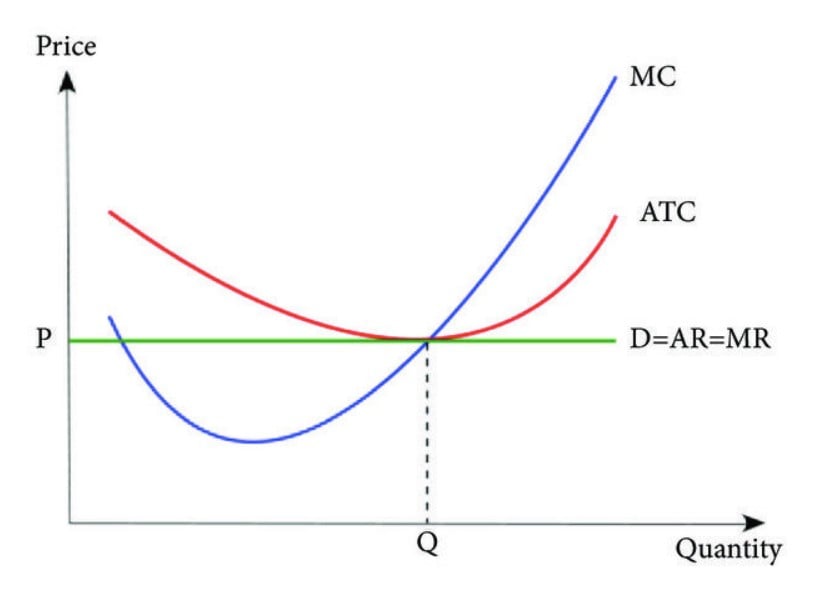
Per economic theory, a company’s profits are maximized at the point on the graph at which its marginal revenue is equivalent to its marginal cost because the net marginal profit is zero.
How to Find Marginal Revenue Curve (MR)
If plotted on an illustrative graph, the break-even point where “MR = MC” is the optimal production level.
Once a company begins to surpass its break-even point of production, it may be time for the company to significantly reduce (or entirely halt) its selling efforts because it no longer makes sense for the company to continue making sales if the marginal benefit decreases with each sale.
By closely tracking marginal revenue over time, a company’s management team can better understand consumer spending patterns and the prevailing market trends.
From there, an informed management team can set prices appropriately based on their understanding of consumer demand, which should contribute to greater profits and improved operating efficiency.
Three Cost Curves (Source: Journal of Applied Mathematics)
How to Analyze Marginal Revenue in Economics?
In economics, the law of diminishing returns states that the yield from increased production volume eventually reduces over time.
Hence, cost-benefit analysis is frequently associated with microeconomics, where many economists theorize about the optimal cost-benefit analysis trade-off and utility maximization in the markets.
- Perfectly Competitive Market → In a perfectly competitive market characterized by no information asymmetry regarding pricing and homogenous products, the marginal benefit is anticipated to remain constant. The companies in such a market could dictate the pricing for their own self-interests, i.e. if one competitor decides to raise its prices, the reaction of consumers would be to opt to purchase from the other market competitors since the products are homogenous.
- Monopolies → On the other hand, the same phenomenon would not be seen in monopolies because of the limited number of companies in the market. The lack of free market forces and overall competition provide the few companies holding a substantial portion of the total market share the ability to set prices, rather than letting consumer demand determine prices.